Guide for Math Majors
Six Majors, each with its own advantages
Our majors are not tied to a particular career. They develop qualities that appeal to a wide range of employers, such as quantitative reasoning, problem-solving, and strong work ethic. The Careers page has specific examples of post-graduation occupations of our majors. That said, there are several ways in which students can align their mathematical education with particular career goals:
- B. S. in Mathematics is the best choice for students planning on graduate studies in mathematics or any graduate program that requires GRE Mathematics subject test.
- Either B.A. or B.S. Mathematics is required for dual program with School of Education leading to NY State teacher certification (they have additional course requirements).
- Students who more closely associate their future with engineering or physics will likely find Applied Mathematics programs a better fit.
- Students who plan on working with data or going to graduate school in Statistics should consider majoring in Statistics.
- Each B.S. degree requires 4 more MAT courses than the corresponding B.A. degree.
- Students interested in the actuarial profession should plan ahead to align their coursework with preparation for actuarial exams and fulfilling the VEE requirements. See the Actuarial section.
Math Department in numbers (updated October 2023)
- 34 full-time faculty members, 15 of them hired in 2010 or later.
- 6 major programs: Mathematics, Applied Mathematics, and Statistics, each available as B.A. (more flexible option) or B.S. (more intense study)
- About 150 undergraduate majors. Many are double majors with Economics, Physics, Engineering, Computer Science, etc.
- 35 courses that can be applied toward Bachelor’s degrees, not counting Independent Study opportunities.
Program descriptions
Overview of Mathematics and Applied Mathematics majors
There are three kinds of requirements; their details are found in the program descriptions linked above.
- Preliminary: five courses.
- Advanced: six courses for B.A., ten courses for B.S.
- Extra-disciplinary (for Applied Mathematics only): one computing course; four science courses or another major or minor.
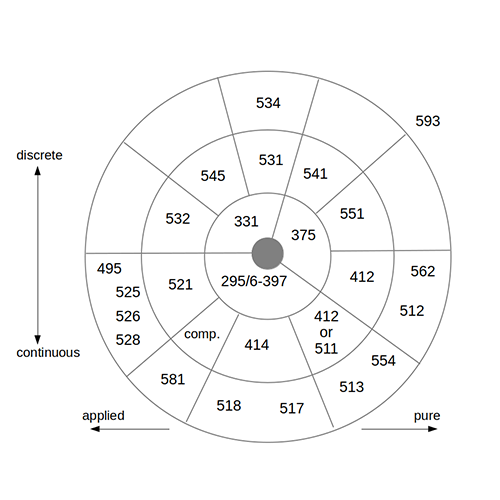
Preliminary courses develop three distinct sets of skills:
- Manipulation with continuous, flexible objects (Calculus)
- Manipulation with discrete or rigid objects (Linear Algebra)
- Formal mathematical reasoning (Introduction to Abstract Mathematics)
Advanced courses draw on all three of the above. They lead to a much deeper understanding of mathematical structures, at the expense of proportionally greater effort. While on the preliminary level students are mostly following instructions, in the advanced courses they develop independent mathematical thought.
Extra-disciplinary requirements are present in both Applied Mathematics programs. They consist of two parts: science courses and computing course. Most students in Applied Mathematics programs satisfy the science part without extra coursework, because they already pursue a qualifying major or minor. The computing requirement takes no extra coursework to Engineering students who already took ECS 102 or ECS 104. Non-Engineering computing courses include CPS 196, PHY 307, and IST 256. Students with programming experience may want to take the more rigorous course CIS 252 instead. Advanced planning is important because the availability of extra-disciplinary courses is not controlled by the Mathematics department, and some of these courses have prerequisites.
Courses
Preliminary
- 295 Calculus I
- 296 Calculus II
- 331 First Course in Linear Algebra
- 375 Introduction to Abstract Mathematics
- 397 Calculus III
Advanced Courses
Having completed the Preliminary courses, students are ready to take any of the following ones:
- 412 Real Analysis I
- 414 Ordinary Differential Equations
- 511 Advanced Calculus
- 521 Probability
- 531 Second Course in Linear Algebra
- 532 Applied Linear Algebra
- 541 Number Theory
- 545 Combinatorics
- 551 Fundamental Concepts of Geometry
- 581 Numerical Methods
Many other advanced courses are available, with subjects ranging from Fundamentals of Data Science and Abstract Algebra to Bayesian Statistics and Differential Geometry.
Overview of Statistics majors
The Statistics programs (B.A. and B.S.) share the same set of preliminary courses, which is slightly different from the Preliminary courses of our other majors:
- 221 Elementary Probability and Statistics I
- 222 Elementary Probability and Statistics II
- 295 Calculus I
- 296 Calculus II
- 331 First Course in Linear Algebra
- 397 Calculus III
- 422 Statistical Computing
After that, students take six advanced courses for B.A. in Statistics or ten advanced courses for B.S. in Statistics. The details are found in the program descriptions linked above.
Getting Involved
Mathematics is far from being a solitary activity. You should get to know the people of Math department, both students and professors. Some suggestions:
- Attend Math Club events. You don’t have to be a Pi Mu Epsilon member (or even a math major) to attend.
- Participate in class discussions.
- Talk to professors during their office hours. Some of them will probably be writing recommendation letters for you. The better they know you, the more effective their letters will be.
- Check out career resources and summer research programs linked in the sidebar.
- Join our LinkedIn group
Beyond the standard coursework
The recommended preparation for mathematics-intensive graduate programs is B.S. in Mathematics, even if you are primarily interested in applied mathematics. You should also strengthen your application file with activities that go beyond the standard curriculum. Some of them are sensible things to do even if you do not plan on going to graduate school:
- If you are taking Calculus (MAT 295, 296, 397), enroll in the Calculus Plus add-on course (MAT 291, 292, 391) where the subject is explored in more depth.
- Apply to the Directed Reading Program which pairs undergraduate students with graduate mentors for a semester-long reading project.
- Apply for Pi Mu Epsilon membership, and consider serving as an officer of our chapter.
- Self-study and/or group-study for Putnam exam, a nationwide college-level mathematics contest which is an opportunity to develop your logical reasoning and problem-solving skills.
- Make sure you are familiar with most of the topics on GRE Mathematics Test, and try some practice problems.
- If you are a non-native speaker of English, be aware that many graduate school recommendation forms will explicitly ask the recommender about the applicant’s mastery of spoken and written English. Do not shy away from conversations.
The following are more serious undertakings which should be discussed with your advisor in advance:
- Take the sequences 412-512 and 531-534 in the junior year. These are hard courses which emphasize proofs and abstract thinking. They are essential for graduate schools preparation, for REU applications, and for getting strong letters of recommendations. If you find that the regular homework in these classes is not challenging enough, talk to your professor, who may be able to suggest harder problems from the textbook or elsewhere.
- Apply to summer research programs (REU) during your junior year. Applications are due early in the Spring semester.
- Take Senior Seminar (599) or Statistics Seminar (598). These senior-level courses may lead to graduation with Distinction.
- Take graduate level classes in the senior year: 601 (after 412-512) or 631 (after 531-534). If you are interested in Statistics, consider 653 (after 521-525).
- Sign up for Independent Study (490) on a subject outside of the standard curriculum. This is contingent on finding a professor who agrees to supervise the study.
- Apply to an undergraduate research grant to support your research project.
- Write a Senior Thesis.
Actuarial focus
There is no separate track for students interested in actuarial work. All four major programs in mathematics are compatible with the focus on future actuarial career.
You should be familiar with the website BeAnActuary.org which is jointly ran by two major actuarial societies. Pay particular attention to the description of the Probability Exam (1/P). Passing this challenging three-hour exam requires thorough command of probability and calculus. The calculus material is contained in our 295-296-397 sequence, but you will need to know more probability theory than is taught in 521. Thus, you should take 521 as early as practical, and follow it with intensive self-study for the exam. Other mathematics courses relevant to actuarial exams are MAT 525 Mathematical Statistics (for Exam 4/C), MAT 526 Stochastic Processes (part of which may be helpful with Exam 1/P), and MAT 528 Probability Models for Actuarial Science.
Another introductory exam that can be passed during college year is Financial Mathematics, Exam 2/FM. Its mathematical content is not sophisticated by math major standards; this exam tests the knowledge of a large number of financial terms and associated formulas. Self-study, guided by the exam syllabus, is the best preparation for it. There are free online sample exams for both 1/P and 2/FM on the Society of Actuaries website.
You should make as much progress toward VEE (Validation by Educational Experience) as possible. The relevant courses are MAT 525 (VEE in Mathematical Statistics), ECN 101, ECN 102, and ECN 203 (VEE in Economics).
Some background in economics, finance or accounting is an advantage in applications for actuarial internships, as well as in preparation for the Financial Mathematics exam 2/FM. If your schedule allows, consider a minor in economics or finance.
You should also be proficient with Microsoft Excel. A number of free tutorials are available online, including some directly from Microsoft. Excel Training and Certification Program is available to A&S and Maxwell students. It is desirable to have some programming experience. Familiarity with database software and experience with writing SQL queries is also a plus.
Miscellaneous
Three major professional societies of U.S. mathematicians are MAA, AMS and SIAM: roughly speaking, they focus on teaching, research and applications, respectively. Each of them maintains a catalog of career resources, which reflects the emphasis of that society.
In addition to general computer proficiency, you may want to develop the skill of translating mathematical ideas into an algorithm solving a particular problem. A rich practice field is Project Euler. Many of these problems are more approachable for students who took 541 or 545 and/or have some computer science background.
